FUNDAMENTALS OF COLLEGE ALGEBRA

Course Description

Algebra—or “al-jabr”— literally means the “reunion of broken parts”. The origin of algebra is traced to the ancient Babylonians and is the unifying thread of almost all of mathematics.

This DSST exam was developed to enable schools to award credit to students for knowledge equivalent to that learned by students taking the course. This exam covers topics such as complex numbers, algebraic operations, equations and inequalities, and properties of functions and their graphs. The use of a non-programmable calculator is permitted in this exam.

Exam Outline

The following is an outline of the content areas covered in the examination. The approximate percentage of the examination devoted to each content area is also noted.

I. Fundamental Algebraic Operations – 20%

1. Operations with algebraic expressions
2. Operations with polynomials (including factoring and expanding polynomials)
3. Rational expressions
4. Operations with positive, negative and fractional exponents

II. Complex Numbers – 4%

1. Conjugate
2. Basic Operations

III. Equations and Inequalities – 44%

1. Linear equations and inequalities
2. Quadratic equations and inequalities (including quadratic forms and solving quadratic inequalities)
3. Absolute value equations and inequalities
4. Systems of linear equations and inequalities
5. Exponential and logarithmic equations
6. Equations involving radicals

IV. Properties of Functions and their Graphs – 32%

1. Coordinate systems
2. Domain and range
3. Operations of functions
4. Inverse functions
5. Linear functions
6. Quadratic functions
7. Polynomial functions
8. Rational functions
9. Exponential and logarithmic functions

Sample Questions

All test questions are in a multiple-choice format, with one correct answer and three incorrect options. The following are samples of the types of questions that may appear on the exam.

1. If x² ≠ 1, then

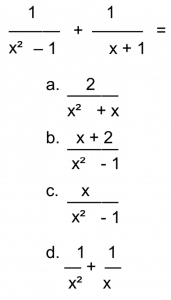
2. Which of the following is a solution of the equation x² + 3x – 2 = 0?

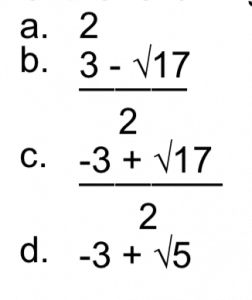
3. An experimental formula for the number of hours of sleep a child needs is S = 13.5 – (y/3), where S is the number of hours of sleep needed and y is the age of the child in years. According to this formula, with each passing year, a child needs:

1. 1/3 hour less sleep
2. 1/3 hour more sleep
3. 1 hour less sleep
4. 1 hour more sleep

4.

. 

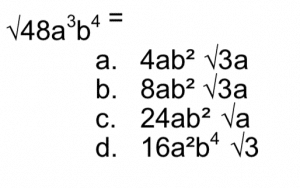
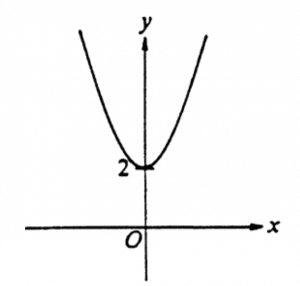
5.  Which of the following could be the equation of the graph below?

1. y = 2 x2
2. y = – x2 + 2
3. y = x2 + 2
4. x=y2 +2